AquaGL: Marching Cubes and Boids

Introduction

This project was created as the final project for a university course focused on linear algebra and scientific computing. Initially, I decided to delve into some graphical programming, making this project my introduction to general graphics programming paradigms and shader code. I began by constructing a crude 3D engine using C++/OpenGL, following the great tutorial series on learnopengl.com. I then implemented the marching cubes algorithm with procedural terrain generation goals in mind. Once I had the terrain, I felt the need to add movement to the scene, leading to the implementation of a boid system to simulate schools of fish.

Marching Cubes

The marching cubes algorithm allows us to define an isosurface in terms of triangles. Which means that if we have a scalar function f(x,y,z) in 3D space, we can, for example, render the surface f(x,y,z)=0 to the screen as an array of triangles that is easily processed by the GPU.

This algorithm has broad applications in various fields that deal with scalar values in space, such as medical imaging, 3D modeling and games. The latter being the direction I decided to move in with the goal of creating a visual demo with randomly generated terrain like the game Minecraft.

Marching cubes works by first dividing the space onto a grid; how fine this grid is will dictate the resolution of your 3D mesh. We iterate over all cubes contained in this grid, and we sample for the scalar values of the function on each vertex of the cube. If our threshold is zero (plotting f(x,y,z)=0) we will check which vertices are inside the surface (sample<0) or outside (sample>0). Here's the catch: since a cube has 8 vertices, we only have 2^8 = 256 cases! So we keep the solution for each case in a 256-long array. Therefore, we don't need to programatically solve the problem; we only need to read the array for the correct case.

The correct solution for each case is a list of edges of the cube. These are the edges which will contain the vertices of our triangles. You could also think of them as the edges that intersect our chosen surface.

In the above image, you can see what some of the case solutions look like. The blue vertices of the cube were labeled as inside the volume enclosed by the surface. The surface's triangle vertices here are placed on the midpoint of each cube edge. As you can imagine, that will create a very pointy surface composed only of 45 and 90-degree angles. So here comes the first hack we can use since we are in a scalar field: interpolation.

Let's say we're looking at an edge where one vertex has a value of 1.0 and the other has a value of -1.0. Then, it would be a good guess that the surface crosses at the midpoint of this edge. But if the values are 1.0 and -0.5, you would be correct to assume that the surface is probably closer to the -0.5 vertex than the other one. With that, we can offset from the midpoint accordingly in order to gain smoother surfaces.

As you can see, the polygonal model on the left has a smooth surface, while the right one is jagged and pointy. The one on the left is using the scalar field values to linearly interpolate the vertex positions. The method used is simple: Calculate the intersection point of a linear function that fits both ends of the edge with the threshold. So if at one end of the cube edge the function value is 1.0 and at the other -0.5, let f(x) = ax + b be the function that has f(0) = 1.0 and f(1) = -0.5. The point of intersection with the threshold is the solution for f(x) = threshold.

Additionally, in order for our mesh to look good, we need it to interact with the light of the scene, and for that we need normals. The standard marching cubes does not contain normal calculations for each vertex, but there is a simple shortcut since we are in a scalar field. Knowing some calculus, you can remember that the normal of our isosurface is basically the gradient vector at that point.

The Boids

Boids is a way to simulate the flocking behavior of birds or schools of fish as found in nature. This was used for some of the fish in the movie Finding Nemo, and it's also being used today in the recent developments of drone swarms. Boids are a great example of one of my favorite things: emergence. AKA, the whole is more than the sum of its parts. This is because birds' flocking patterns are complex time-spatial structures, and the boid algorithm does not have to deal with such complexities to reproduce them. Each bird is independent and makes decisions on its direction by itself. We only need to code the individual behavior of each boid and the schoolling will naturally emerge from the simulation! Each boid behaves by a set of rules:

1. Cohesion

Each boid tries to move towards the average position of every other boid in his viewing range.

2. Separation

Each boid tries to keep a distance from each other boid in it's viewing range so they don't clutter up.

3. Alignment

Each boid tries to move in the same average direction in which all boids in its viewing range are moving.

4. Obstacle avoidance

Boids try to avoid obstacles they see so as not to collide or pass through terrain.

Obstacle avoidance is normally conducted by raycasting in multiple directions in front of the boid so as to check for collisions. If collisions are detected, the boid will move towards the furthest unblocked ray from the collisions. This is complicated and increases the resource demand of our program. But there's a clever shortcut: since we are in a scalar field, we can use the gradient of the field. We know that the gradient will always point in the greatest direction of function value increase, so by following this direction, we will be steering away from the isosurface at the given threshold. Here's a diagram:

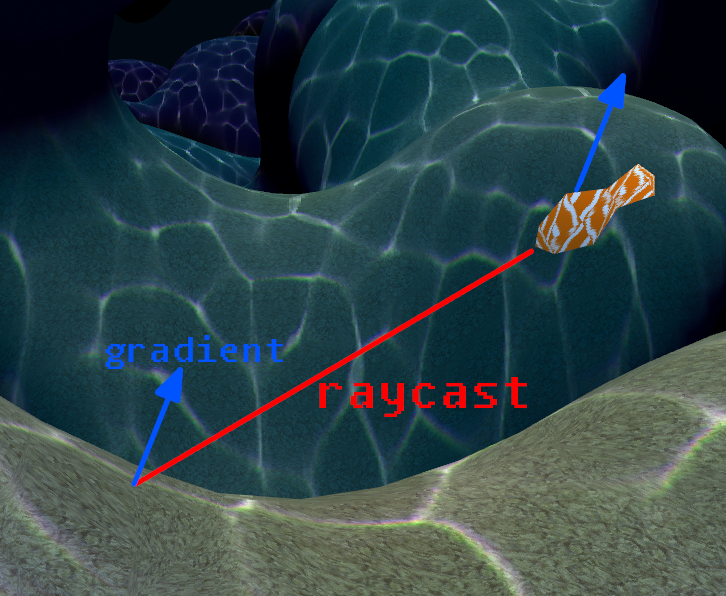
I have also added, for fun, a predator fish. He moves in the direction of the fish in his view, and all the fish will try to run away from him.

To make the clownfish swimming animation I altered their vertex shader to add a sine function along the direction of movement to the vertex positions of the model. This sine function is modulated by the simulation time so as to make every vertex of the model sway with time.

Water Caustics

You know those bright scintilating lines you see at the bottom of a pool? Those are called caustics; they are caused by the turbulent waves on the surface of the water acting as lenses that can refract the light of the sun in different ways. Simulating them in real time can get very complicated, as you would also need a water simulation just to get those lensing waves. Since I wanted a 'cheap' way to get an underwater look to the scene I decided upon the fake caustics method.

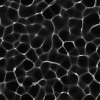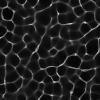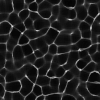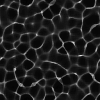
Fake caustics are very simple, you have an animated texture of caustics that loops, then project the animated texture onto the scene from the point of view of the light source and modulate the texture brightness at each point to match the amount of light received by the surface.

Since each wavelength of light has a different refraction index, the caustics seem in real life are often colorful and rainbow-like. Since the program I used to generate the caustics texture was only black and white, I displaced each color channel (RGB) of the texture by a different amount in the fragment shader code. This is a cheap way to get a very convincing rainbow effect, even if it's physically inaccurate.

Conclusion

By adhering to low-level graphics programming, I have created a portable and light-weight virtual aquarium. This program could easily be expanded into a video game or a simulation of wild life. Things that could be done to further enhance this program is a method to load models. The fish model was created using the same method as the terrain (marching cubes), so it's very limited. Also, major performance boosts could be achieved by leveling the boid system's computations to the GPU with compute shaders.

On the subject of fish life simulations, I could add anemonae, which clownfish in nature form a symbiotic relationship with. The boids would be attracted to the anemone and possible predators wouldn't be able to chase them since the anemone stings. This could make AquaGL even more interesting to watch.

The source code for this project is available here